numpy.cross()

Return the cross product of two (arrays of) vectors.

The cross product of a and b in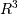 is a vector perpendicular to both a and b. If a and b are arrays of vectors, the vectors are defined by the last axis of a and b by default, and these axes can have dimensions 2 or 3. Where the dimension of either a or b is 2, the third component of the input vector is assumed to be zero and the cross product calculated accordingly. In cases where both input vectors have dimension 2, the z-component of the cross product is returned.

Notes

Supports full broadcasting of the inputs.

Examples

Vector cross-product.

>>> x = [1, 2, 3]
>>> y = [4, 5, 6]
>>> np.cross(x, y)
array([-3,  6, -3])

One vector with dimension 2.

>>> x = [1, 2]
>>> y = [4, 5, 6]
>>> np.cross(x, y)
array([12, -6, -3])

Equivalently:

>>> x = [1, 2, 0]
>>> y = [4, 5, 6]
>>> np.cross(x, y)
array([12, -6, -3])

Both vectors with dimension 2.

>>> x = [1,2]
>>> y = [4,5]
>>> np.cross(x, y)
-3

Multiple vector cross-products. Note that the direction of the cross product vector is defined by the right-hand rule.

>>> x = np.array([[1,2,3], [4,5,6]])
>>> y = np.array([[4,5,6], [1,2,3]])
>>> np.cross(x, y)
array([[-3,  6, -3],
       [ 3, -6,  3]])

The orientation of c can be changed using the axisc keyword.

>>> np.cross(x, y, axisc=0)
array([[-3,  3],
       [ 6, -6],
       [-3,  3]])

Change the vector definition of x and y using axisa and axisb.

>>> x = np.array([[1,2,3], [4,5,6], [7, 8, 9]])
>>> y = np.array([[7, 8, 9], [4,5,6], [1,2,3]])
>>> np.cross(x, y)
array([[ -6,  12,  -6],
       [  0,   0,   0],
       [  6, -12,   6]])
>>> np.cross(x, y, axisa=0, axisb=0)
array([[-24,  48, -24],
       [-30,  60, -30],
       [-36,  72, -36]])