-
numpy.polynomial.chebyshev.chebval2d(x, y, c)[source] -
Evaluate a 2-D Chebyshev series at points (x, y).
This function returns the values:
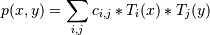
The parameters
xandyare converted to arrays only if they are tuples or a lists, otherwise they are treated as a scalars and they must have the same shape after conversion. In either case, eitherxandyor their elements must support multiplication and addition both with themselves and with the elements ofc.If
cis a 1-D array a one is implicitly appended to its shape to make it 2-D. The shape of the result will be c.shape[2:] + x.shape.Parameters: x, y : array_like, compatible objects
The two dimensional series is evaluated at the points
(x, y), wherexandymust have the same shape. Ifxoryis a list or tuple, it is first converted to an ndarray, otherwise it is left unchanged and if it isn?t an ndarray it is treated as a scalar.c : array_like
Array of coefficients ordered so that the coefficient of the term of multi-degree i,j is contained in
c[i,j]. Ifchas dimension greater than 2 the remaining indices enumerate multiple sets of coefficients.Returns: values : ndarray, compatible object
The values of the two dimensional Chebyshev series at points formed from pairs of corresponding values from
xandy.See also
Notes
numpy.polynomial.chebyshev.chebval2d()
2025-01-10 15:47:30
Please login to continue.