-
numpy.polynomial.polynomial.polyfromroots(roots)[source] -
Generate a monic polynomial with given roots.
Return the coefficients of the polynomial
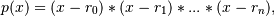
where the
r_nare the roots specified inroots. If a zero has multiplicity n, then it must appear inrootsn times. For instance, if 2 is a root of multiplicity three and 3 is a root of multiplicity 2, thenrootslooks something like [2, 2, 2, 3, 3]. The roots can appear in any order.If the returned coefficients are
c, then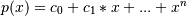
The coefficient of the last term is 1 for monic polynomials in this form.
Parameters: roots : array_like
Sequence containing the roots.
Returns: out : ndarray
1-D array of the polynomial?s coefficients If all the roots are real, then
outis also real, otherwise it is complex. (see Examples below).See also
chebfromroots,legfromroots,lagfromroots,hermfromroots,hermefromrootsNotes
The coefficients are determined by multiplying together linear factors of the form
(x - r_i), i.e.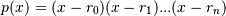
where
n == len(roots) - 1; note that this implies that1is always returned for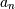 .
.Examples
>>> from numpy.polynomial import polynomial as P >>> P.polyfromroots((-1,0,1)) # x(x - 1)(x + 1) = x^3 - x array([ 0., -1., 0., 1.]) >>> j = complex(0,1) >>> P.polyfromroots((-j,j)) # complex returned, though values are real array([ 1.+0.j, 0.+0.j, 1.+0.j])
numpy.polynomial.polynomial.polyfromroots()
2025-01-10 15:47:30
Please login to continue.