-
numpy.polynomial.polynomial.polyval(x, c, tensor=True)[source] -
Evaluate a polynomial at points x.
If
cis of lengthn + 1, this function returns the value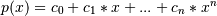
The parameter
xis converted to an array only if it is a tuple or a list, otherwise it is treated as a scalar. In either case, eitherxor its elements must support multiplication and addition both with themselves and with the elements ofc.If
cis a 1-D array, thenp(x)will have the same shape asx. Ifcis multidimensional, then the shape of the result depends on the value oftensor. Iftensoris true the shape will be c.shape[1:] + x.shape. Iftensoris false the shape will be c.shape[1:]. Note that scalars have shape (,).Trailing zeros in the coefficients will be used in the evaluation, so they should be avoided if efficiency is a concern.
Parameters: x : array_like, compatible object
If
xis a list or tuple, it is converted to an ndarray, otherwise it is left unchanged and treated as a scalar. In either case,xor its elements must support addition and multiplication with with themselves and with the elements ofc.c : array_like
Array of coefficients ordered so that the coefficients for terms of degree n are contained in c[n]. If
cis multidimensional the remaining indices enumerate multiple polynomials. In the two dimensional case the coefficients may be thought of as stored in the columns ofc.tensor : boolean, optional
If True, the shape of the coefficient array is extended with ones on the right, one for each dimension of
x. Scalars have dimension 0 for this action. The result is that every column of coefficients incis evaluated for every element ofx. If False,xis broadcast over the columns ofcfor the evaluation. This keyword is useful whencis multidimensional. The default value is True.New in version 1.7.0.
Returns: values : ndarray, compatible object
The shape of the returned array is described above.
See also
Notes
The evaluation uses Horner?s method.
Examples
>>> from numpy.polynomial.polynomial import polyval >>> polyval(1, [1,2,3]) 6.0 >>> a = np.arange(4).reshape(2,2) >>> a array([[0, 1], [2, 3]]) >>> polyval(a, [1,2,3]) array([[ 1., 6.], [ 17., 34.]]) >>> coef = np.arange(4).reshape(2,2) # multidimensional coefficients >>> coef array([[0, 1], [2, 3]]) >>> polyval([1,2], coef, tensor=True) array([[ 2., 4.], [ 4., 7.]]) >>> polyval([1,2], coef, tensor=False) array([ 2., 7.])
numpy.polynomial.polynomial.polyval()
2025-01-10 15:47:30
Please login to continue.