The PCA does an unsupervised dimensionality reduction, while the logistic regression does the prediction.
We use a GridSearchCV to set the dimensionality of the PCA
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | print(__doc__)# Code source: Ga Varoquaux# Modified for documentation by Jaques Grobler# License: BSD 3 clauseimport numpy as npimport matplotlib.pyplot as pltfrom sklearn import linear_model, decomposition, datasetsfrom sklearn.pipeline import Pipelinefrom sklearn.model_selection import GridSearchCVlogistic = linear_model.LogisticRegression()pca = decomposition.PCA()pipe = Pipeline(steps=[('pca', pca), ('logistic', logistic)])digits = datasets.load_digits()X_digits = digits.datay_digits = digits.target |
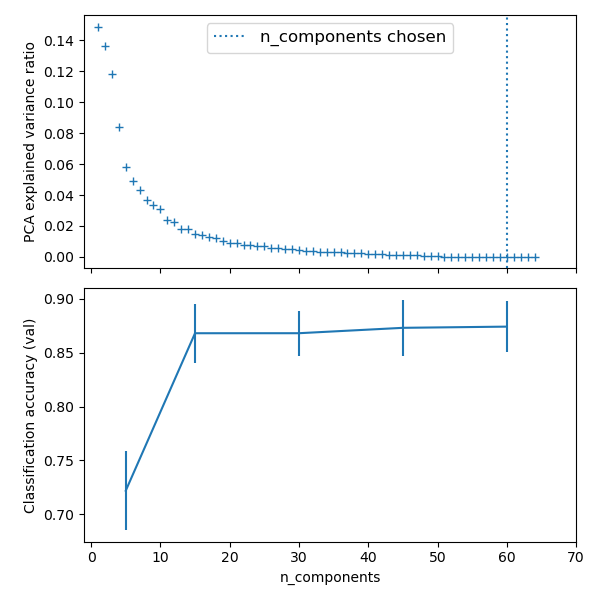
Plot the PCA spectrum
1 2 3 4 5 6 7 8 9 | pca.fit(X_digits)plt.figure(1, figsize=(4, 3))plt.clf()plt.axes([.2, .2, .7, .7])plt.plot(pca.explained_variance_, linewidth=2)plt.axis('tight')plt.xlabel('n_components')plt.ylabel('explained_variance_') |
Prediction
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | n_components = [20, 40, 64]Cs = np.logspace(-4, 4, 3)#Parameters of pipelines can be set using ?__? separated parameter names:estimator = GridSearchCV(pipe, dict(pca__n_components=n_components, logistic__C=Cs))estimator.fit(X_digits, y_digits)plt.axvline(estimator.best_estimator_.named_steps['pca'].n_components, linestyle=':', label='n_components chosen')plt.legend(prop=dict(size=12))plt.show() |
Total running time of the script: (0 minutes 9.258 seconds)
Download Python source code:
plot_digits_pipe.py
Download IPython notebook:
plot_digits_pipe.ipynb
Please login to continue.