Lasso and elastic net (L1 and L2 penalisation) implemented using a coordinate descent.
The coefficients can be forced to be positive.
Out:
1 2 3 4 | Computing regularization path using the lasso...Computing regularization path using the positive lasso...Computing regularization path using the elastic net...Computing regularization path using the positive elastic net... |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 | print(__doc__)# Author: Alexandre Gramfort <alexandre.gramfort@inria.fr># License: BSD 3 clausefrom itertools import cycleimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import lasso_path, enet_pathfrom sklearn import datasetsdiabetes = datasets.load_diabetes()X = diabetes.datay = diabetes.targetX /= X.std(axis=0) # Standardize data (easier to set the l1_ratio parameter)# Compute pathseps = 5e-3 # the smaller it is the longer is the pathprint("Computing regularization path using the lasso...")alphas_lasso, coefs_lasso, _ = lasso_path(X, y, eps, fit_intercept=False)print("Computing regularization path using the positive lasso...")alphas_positive_lasso, coefs_positive_lasso, _ = lasso_path( X, y, eps, positive=True, fit_intercept=False)print("Computing regularization path using the elastic net...")alphas_enet, coefs_enet, _ = enet_path( X, y, eps=eps, l1_ratio=0.8, fit_intercept=False)print("Computing regularization path using the positive elastic net...")alphas_positive_enet, coefs_positive_enet, _ = enet_path( X, y, eps=eps, l1_ratio=0.8, positive=True, fit_intercept=False)# Display resultsplt.figure(1)ax = plt.gca()colors = cycle(['b', 'r', 'g', 'c', 'k'])neg_log_alphas_lasso = -np.log10(alphas_lasso)neg_log_alphas_enet = -np.log10(alphas_enet)for coef_l, coef_e, c in zip(coefs_lasso, coefs_enet, colors): l1 = plt.plot(neg_log_alphas_lasso, coef_l, c=c) l2 = plt.plot(neg_log_alphas_enet, coef_e, linestyle='--', c=c)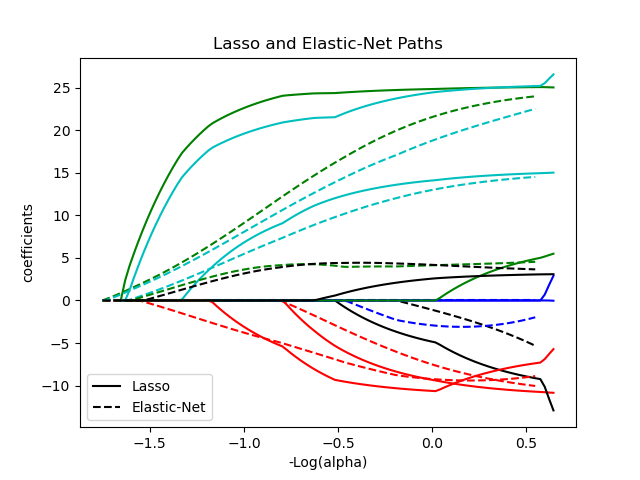plt.xlabel('-Log(alpha)')plt.ylabel('coefficients')plt.title('Lasso and Elastic-Net Paths')plt.legend((l1[-1], l2[-1]), ('Lasso', 'Elastic-Net'), loc='lower left')plt.axis('tight')plt.figure(2)ax = plt.gca()neg_log_alphas_positive_lasso = -np.log10(alphas_positive_lasso)for coef_l, coef_pl, c in zip(coefs_lasso, coefs_positive_lasso, colors): l1 = plt.plot(neg_log_alphas_lasso, coef_l, c=c) l2 = plt.plot(neg_log_alphas_positive_lasso, coef_pl, linestyle='--', c=c)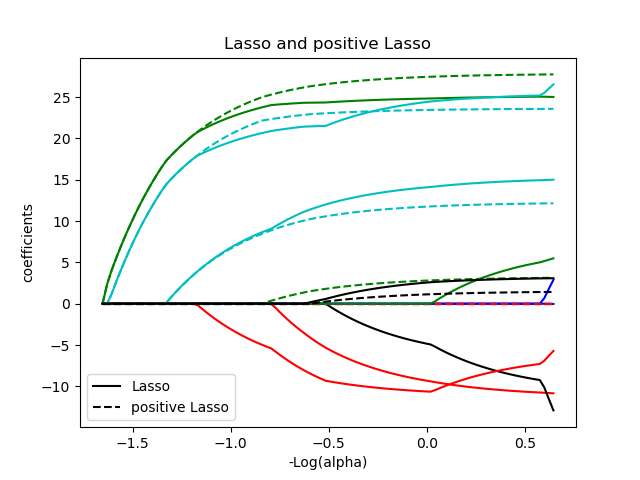plt.xlabel('-Log(alpha)')plt.ylabel('coefficients')plt.title('Lasso and positive Lasso')plt.legend((l1[-1], l2[-1]), ('Lasso', 'positive Lasso'), loc='lower left')plt.axis('tight')plt.figure(3)ax = plt.gca()neg_log_alphas_positive_enet = -np.log10(alphas_positive_enet)for (coef_e, coef_pe, c) in zip(coefs_enet, coefs_positive_enet, colors): l1 = plt.plot(neg_log_alphas_enet, coef_e, c=c) l2 = plt.plot(neg_log_alphas_positive_enet, coef_pe, linestyle='--', c=c)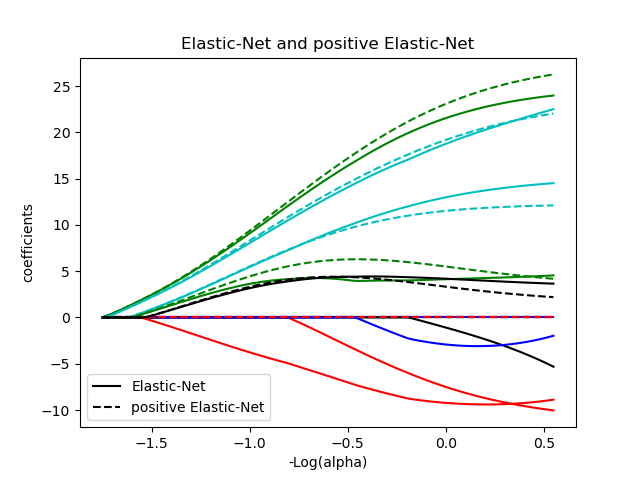plt.xlabel('-Log(alpha)')plt.ylabel('coefficients')plt.title('Elastic-Net and positive Elastic-Net')plt.legend((l1[-1], l2[-1]), ('Elastic-Net', 'positive Elastic-Net'), loc='lower left')plt.axis('tight')plt.show() |
Total running time of the script: (0 minutes 0.408 seconds)
Download Python source code:
plot_lasso_coordinate_descent_path.py
Download IPython notebook:
plot_lasso_coordinate_descent_path.ipynb
Please login to continue.