numpy.random.exponential()

numpy.random.exponential(scale=1.0, size=None)

Draw samples from an exponential distribution.

Its probability density function is

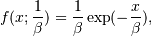
$f(x; \frac{1}{\beta}) = \frac{1}{\beta} \exp(-\frac{x}{\beta}),$

for x > 0 and 0 elsewhere.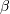 $\beta$ is the scale parameter, which is the inverse of the rate parameter $\lambda = 1/\beta$ . The rate parameter is an alternative, widely used parameterization of the exponential distribution [R218].

The exponential distribution is a continuous analogue of the geometric distribution. It describes many common situations, such as the size of raindrops measured over many rainstorms [R216], or the time between page requests to Wikipedia [R217].

Parameters:

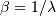Parameters:	scale : float The scale parameter, $\beta = 1/\lambda$ . size : int or tuple of ints, optional Output shape. If the given shape is, e.g., `(m, n, k)`, then `m * n * k` samples are drawn. Default is None, in which case a single value is returned.

scale : float

The scale parameter, $\beta = 1/\lambda$ .

size : int or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. Default is None, in which case a single value is returned.

References

[R216]

(1, 2) Peyton Z. Peebles Jr., ?Probability, Random Variables and Random Signal Principles?, 4th ed, 2001, p. 57.

[R217]

(1, 2) ?Poisson Process?, Wikipedia, http://en.wikipedia.org/wiki/Poisson_process

[R218]

(1, 2) ?Exponential Distribution, Wikipedia, http://en.wikipedia.org/wiki/Exponential_distribution

Links:

https://docs.scipy.org/doc/numpy-1.11.0/reference/generated/numpy.random.exponential.html

doc_NumPy

2017-01-10 18:18:00

Comments