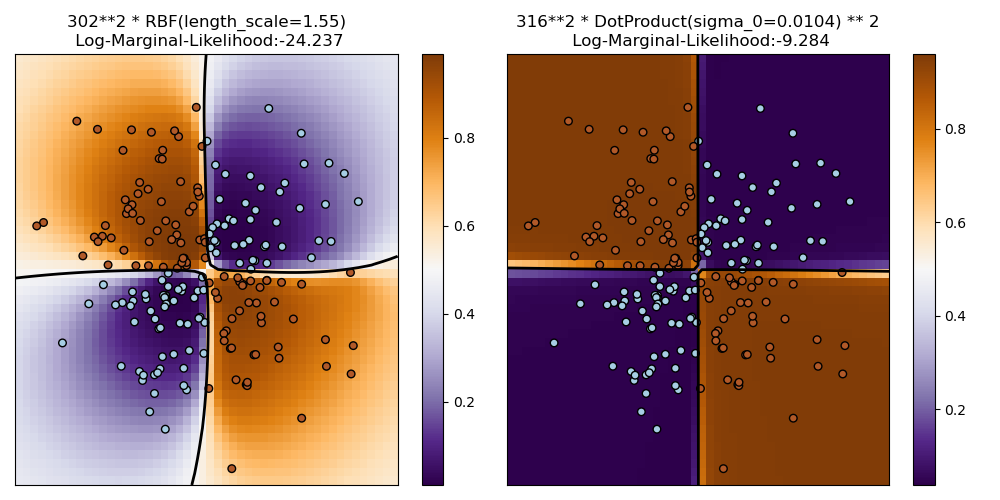
This example illustrates GPC on XOR data. Compared are a stationary, isotropic kernel (RBF) and a non-stationary kernel (DotProduct). On this particular dataset, the DotProduct kernel obtains considerably better results because the class-boundaries are linear and coincide with the coordinate axes. In general, stationary kernels often obtain better results.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | print(__doc__)# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>## License: BSD 3 clauseimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.gaussian_process import GaussianProcessClassifierfrom sklearn.gaussian_process.kernels import RBF, DotProductxx, yy = np.meshgrid(np.linspace(-3, 3, 50), np.linspace(-3, 3, 50))rng = np.random.RandomState(0)X = rng.randn(200, 2)Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)# fit the modelplt.figure(figsize=(10, 5))kernels = [1.0 * RBF(length_scale=1.0), 1.0 * DotProduct(sigma_0=1.0)**2]for i, kernel in enumerate(kernels): clf = GaussianProcessClassifier(kernel=kernel, warm_start=True).fit(X, Y) # plot the decision function for each datapoint on the grid Z = clf.predict_proba(np.vstack((xx.ravel(), yy.ravel())).T)[:, 1] Z = Z.reshape(xx.shape) plt.subplot(1, 2, i + 1) image = plt.imshow(Z, interpolation='nearest', extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto', origin='lower', cmap=plt.cm.PuOr_r) contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2, linetypes='--') plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired) plt.xticks(()) plt.yticks(()) plt.axis([-3, 3, -3, 3]) plt.colorbar(image) plt.title("%s\n Log-Marginal-Likelihood:%.3f" % (clf.kernel_, clf.log_marginal_likelihood(clf.kernel_.theta)), fontsize=12)plt.tight_layout()plt.show() |
Total running time of the script: (0 minutes 1.002 seconds)
Download Python source code:
plot_gpc_xor.py
Download IPython notebook:
plot_gpc_xor.ipynb
Please login to continue.