The usual covariance maximum likelihood estimate can be regularized using shrinkage. Ledoit and Wolf proposed a close formula to compute the asymptotically optimal shrinkage parameter (minimizing a MSE criterion), yielding the Ledoit-Wolf covariance estimate.
Chen et al. proposed an improvement of the Ledoit-Wolf shrinkage parameter, the OAS coefficient, whose convergence is significantly better under the assumption that the data are Gaussian.
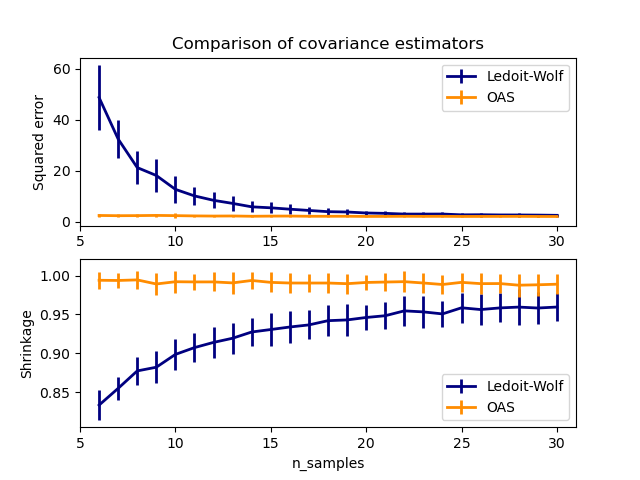
This example, inspired from Chen?s publication [1], shows a comparison of the estimated MSE of the LW and OAS methods, using Gaussian distributed data.
[1] ?Shrinkage Algorithms for MMSE Covariance Estimation? Chen et al., IEEE Trans. on Sign. Proc., Volume 58, Issue 10, October 2010.
1 2 3 4 5 6 7 8 9 | print(__doc__)import numpy as npimport matplotlib.pyplot as pltfrom scipy.linalg import toeplitz, choleskyfrom sklearn.covariance import LedoitWolf, OASnp.random.seed(0) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | n_features = 100# simulation covariance matrix (AR(1) process)r = 0.1real_cov = toeplitz(r ** np.arange(n_features))coloring_matrix = cholesky(real_cov)n_samples_range = np.arange(6, 31, 1)repeat = 100lw_mse = np.zeros((n_samples_range.size, repeat))oa_mse = np.zeros((n_samples_range.size, repeat))lw_shrinkage = np.zeros((n_samples_range.size, repeat))oa_shrinkage = np.zeros((n_samples_range.size, repeat))for i, n_samples in enumerate(n_samples_range): for j in range(repeat): X = np.dot( np.random.normal(size=(n_samples, n_features)), coloring_matrix.T) lw = LedoitWolf(store_precision=False, assume_centered=True) lw.fit(X) lw_mse[i, j] = lw.error_norm(real_cov, scaling=False) lw_shrinkage[i, j] = lw.shrinkage_ oa = OAS(store_precision=False, assume_centered=True) oa.fit(X) oa_mse[i, j] = oa.error_norm(real_cov, scaling=False) oa_shrinkage[i, j] = oa.shrinkage_# plot MSEplt.subplot(2, 1, 1)plt.errorbar(n_samples_range, lw_mse.mean(1), yerr=lw_mse.std(1), label='Ledoit-Wolf', color='navy', lw=2)plt.errorbar(n_samples_range, oa_mse.mean(1), yerr=oa_mse.std(1), label='OAS', color='darkorange', lw=2)plt.ylabel("Squared error")plt.legend(loc="upper right")plt.title("Comparison of covariance estimators")plt.xlim(5, 31)# plot shrinkage coefficientplt.subplot(2, 1, 2)plt.errorbar(n_samples_range, lw_shrinkage.mean(1), yerr=lw_shrinkage.std(1), label='Ledoit-Wolf', color='navy', lw=2)plt.errorbar(n_samples_range, oa_shrinkage.mean(1), yerr=oa_shrinkage.std(1), label='OAS', color='darkorange', lw=2)plt.xlabel("n_samples")plt.ylabel("Shrinkage")plt.legend(loc="lower right")plt.ylim(plt.ylim()[0], 1. + (plt.ylim()[1] - plt.ylim()[0]) / 10.)plt.xlim(5, 31)plt.show() |
Total running time of the script: (0 minutes 3.318 seconds)
plot_lw_vs_oas.py
plot_lw_vs_oas.ipynb
Please login to continue.