Shrinkage covariance estimation

When working with covariance estimation, the usual approach is to use a maximum likelihood estimator, such as the sklearn.covariance.EmpiricalCovariance. It is unbiased, i.e. it converges to the true (population) covariance when given many observations. However, it can also be beneficial to regularize it, in order to reduce its variance; this, in turn, introduces some bias. This example illustrates the simple regularization used in Shrunk Covariance estimators. In particular, it focuses on how to set the amount of regularization, i.e. how to choose the bias-variance trade-off.

Here we compare 3 approaches:

• Setting the parameter by cross-validating the likelihood on three folds according to a grid of potential shrinkage parameters.
• A close formula proposed by Ledoit and Wolf to compute the asymptotically optimal regularization parameter (minimizing a MSE criterion), yielding the sklearn.covariance.LedoitWolf covariance estimate.
• An improvement of the Ledoit-Wolf shrinkage, the sklearn.covariance.OAS, proposed by Chen et al. Its convergence is significantly better under the assumption that the data are Gaussian, in particular for small samples.

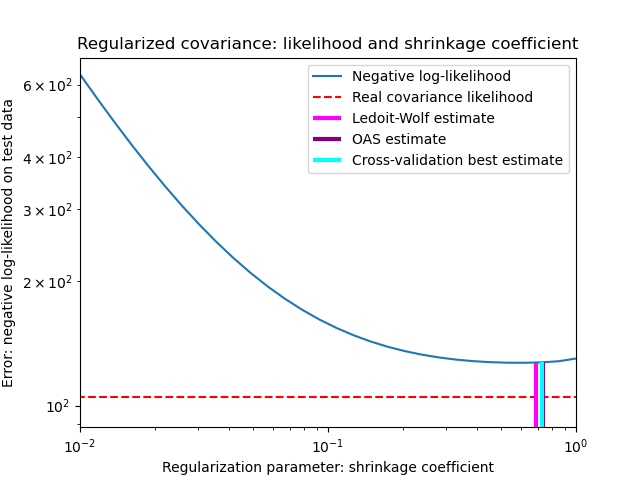
To quantify estimation error, we plot the likelihood of unseen data for different values of the shrinkage parameter. We also show the choices by cross-validation, or with the LedoitWolf and OAS estimates.

Note that the maximum likelihood estimate corresponds to no shrinkage, and thus performs poorly. The Ledoit-Wolf estimate performs really well, as it is close to the optimal and is computational not costly. In this example, the OAS estimate is a bit further away. Interestingly, both approaches outperform cross-validation, which is significantly most computationally costly.

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg

from sklearn.covariance import LedoitWolf, OAS, ShrunkCovariance, \
    log_likelihood, empirical_covariance
from sklearn.model_selection import GridSearchCV

Generate sample data

n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))

# Color samples
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)

Compute the likelihood on test data

# spanning a range of possible shrinkage coefficient values
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [-ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test)
                    for s in shrinkages]

# under the ground-truth model, which we would not have access to in real
# settings
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))

Compare different approaches to setting the parameter

# GridSearch for an optimal shrinkage coefficient
tuned_parameters = [{'shrinkage': shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)

# Ledoit-Wolf optimal shrinkage coefficient estimate
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)

# OAS coefficient estimate
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)

Plot results

fig = plt.figure()
plt.title("Regularized covariance: likelihood and shrinkage coefficient")
plt.xlabel('Regularizaton parameter: shrinkage coefficient')
plt.ylabel('Error: negative log-likelihood on test data')
# range shrinkage curve
plt.loglog(shrinkages, negative_logliks, label="Negative log-likelihood")

plt.plot(plt.xlim(), 2 * [loglik_real], '--r',
         label="Real covariance likelihood")

# adjust view
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6. * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10. * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# LW likelihood
plt.vlines(lw.shrinkage_, ymin, -loglik_lw, color='magenta',
           linewidth=3, label='Ledoit-Wolf estimate')
# OAS likelihood
plt.vlines(oa.shrinkage_, ymin, -loglik_oa, color='purple',
           linewidth=3, label='OAS estimate')
# best CV estimator likelihood
plt.vlines(cv.best_estimator_.shrinkage, ymin,
           -cv.best_estimator_.score(X_test), color='cyan',
           linewidth=3, label='Cross-validation best estimate')

plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()

plt.show()

Total running time of the script: (0 minutes 0.424 seconds)