-
class sklearn.gaussian_process.kernels.RationalQuadratic(length_scale=1.0, alpha=1.0, length_scale_bounds=(1e-05, 100000.0), alpha_bounds=(1e-05, 100000.0))[source] -
Rational Quadratic kernel.
The RationalQuadratic kernel can be seen as a scale mixture (an infinite sum) of RBF kernels with different characteristic length-scales. It is parameterized by a length-scale parameter length_scale>0 and a scale mixture parameter alpha>0. Only the isotropic variant where length_scale is a scalar is supported at the moment. The kernel given by:
k(x_i, x_j) = (1 + d(x_i, x_j)^2 / (2*alpha * length_scale^2))^-alpha
New in version 0.18.
Parameters: length_scale : float > 0, default: 1.0
The length scale of the kernel.
alpha : float > 0, default: 1.0
Scale mixture parameter
length_scale_bounds : pair of floats >= 0, default: (1e-5, 1e5)
The lower and upper bound on length_scale
alpha_bounds : pair of floats >= 0, default: (1e-5, 1e5)
The lower and upper bound on alpha
Methods
clone_with_theta(theta)Returns a clone of self with given hyperparameters theta. diag(X)Returns the diagonal of the kernel k(X, X). get_params([deep])Get parameters of this kernel. is_stationary()Returns whether the kernel is stationary. set_params(\*\*params)Set the parameters of this kernel. -
__init__(length_scale=1.0, alpha=1.0, length_scale_bounds=(1e-05, 100000.0), alpha_bounds=(1e-05, 100000.0))[source]
-
bounds -
Returns the log-transformed bounds on the theta.
Returns: bounds : array, shape (n_dims, 2)
The log-transformed bounds on the kernel?s hyperparameters theta
-
clone_with_theta(theta)[source] -
Returns a clone of self with given hyperparameters theta.
-
diag(X)[source] -
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.
Parameters: X : array, shape (n_samples_X, n_features)
Left argument of the returned kernel k(X, Y)
Returns: K_diag : array, shape (n_samples_X,)
Diagonal of kernel k(X, X)
-
get_params(deep=True)[source] -
Get parameters of this kernel.
Parameters: deep: boolean, optional :
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
-
hyperparameters -
Returns a list of all hyperparameter specifications.
-
is_stationary()[source] -
Returns whether the kernel is stationary.
-
n_dims -
Returns the number of non-fixed hyperparameters of the kernel.
-
set_params(**params)[source] -
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form
<component>__<parameter>so that it?s possible to update each component of a nested object.Returns: self :
-
theta -
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel?s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
Returns: theta : array, shape (n_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
-
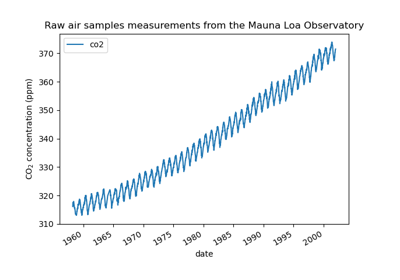
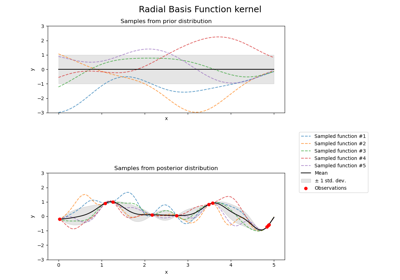
gaussian_process.kernels.RationalQuadratic()
Examples using
2025-01-10 15:47:30
Please login to continue.