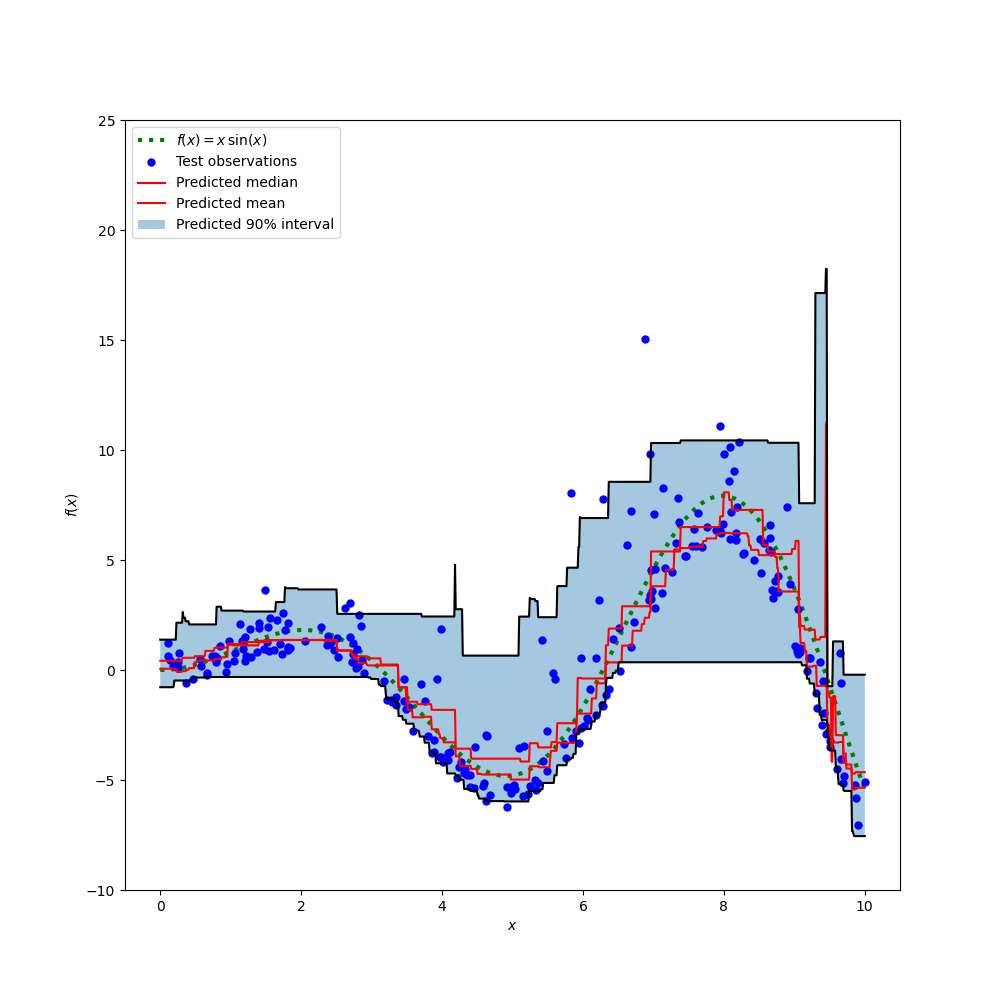
This example shows how quantile regression can be used to create prediction intervals.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 | import numpy as npimport matplotlib.pyplot as pltfrom sklearn.ensemble import GradientBoostingRegressornp.random.seed(1)def f(x): """The function to predict.""" return x * np.sin(x)#----------------------------------------------------------------------# First the noiseless caseX = np.atleast_2d(np.random.uniform(0, 10.0, size=100)).TX = X.astype(np.float32)# Observationsy = f(X).ravel()dy = 1.5 + 1.0 * np.random.random(y.shape)noise = np.random.normal(0, dy)y += noisey = y.astype(np.float32)# Mesh the input space for evaluations of the real function, the prediction and# its MSExx = np.atleast_2d(np.linspace(0, 10, 1000)).Txx = xx.astype(np.float32)alpha = 0.95clf = GradientBoostingRegressor(loss='quantile', alpha=alpha, n_estimators=250, max_depth=3, learning_rate=.1, min_samples_leaf=9, min_samples_split=9)clf.fit(X, y)# Make the prediction on the meshed x-axisy_upper = clf.predict(xx)clf.set_params(alpha=1.0 - alpha)clf.fit(X, y)# Make the prediction on the meshed x-axisy_lower = clf.predict(xx)clf.set_params(loss='ls')clf.fit(X, y)# Make the prediction on the meshed x-axisy_pred = clf.predict(xx)# Plot the function, the prediction and the 90% confidence interval based on# the MSEfig = plt.figure()plt.plot(xx, f(xx), 'g:', label=u'$f(x) = x\,\sin(x)$')plt.plot(X, y, 'b.', markersize=10, label=u'Observations')plt.plot(xx, y_pred, 'r-', label=u'Prediction')plt.plot(xx, y_upper, 'k-')plt.plot(xx, y_lower, 'k-')plt.fill(np.concatenate([xx, xx[::-1]]), np.concatenate([y_upper, y_lower[::-1]]), alpha=.5, fc='b', ec='None', label='90% prediction interval')plt.xlabel('$x$')plt.ylabel('$f(x)$')plt.ylim(-10, 20)plt.legend(loc='upper left')plt.show() |
Total running time of the script: (0 minutes 0.311 seconds)
Download Python source code:
plot_gradient_boosting_quantile.py
Download IPython notebook:
plot_gradient_boosting_quantile.ipynb
Please login to continue.