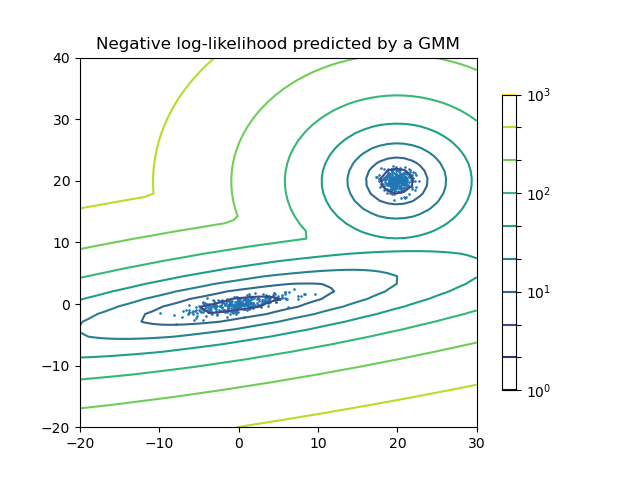
Plot the density estimation of a mixture of two Gaussians. Data is generated from two Gaussians with different centers and covariance matrices.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | import numpy as npimport matplotlib.pyplot as pltfrom matplotlib.colors import LogNormfrom sklearn import mixturen_samples = 300# generate random sample, two componentsnp.random.seed(0)# generate spherical data centered on (20, 20)shifted_gaussian = np.random.randn(n_samples, 2) + np.array([20, 20])# generate zero centered stretched Gaussian dataC = np.array([[0., -0.7], [3.5, .7]])stretched_gaussian = np.dot(np.random.randn(n_samples, 2), C)# concatenate the two datasets into the final training setX_train = np.vstack([shifted_gaussian, stretched_gaussian])# fit a Gaussian Mixture Model with two componentsclf = mixture.GaussianMixture(n_components=2, covariance_type='full')clf.fit(X_train)# display predicted scores by the model as a contour plotx = np.linspace(-20., 30.)y = np.linspace(-20., 40.)X, Y = np.meshgrid(x, y)XX = np.array([X.ravel(), Y.ravel()]).TZ = -clf.score_samples(XX)Z = Z.reshape(X.shape)CS = plt.contour(X, Y, Z, norm=LogNorm(vmin=1.0, vmax=1000.0), levels=np.logspace(0, 3, 10))CB = plt.colorbar(CS, shrink=0.8, extend='both')plt.scatter(X_train[:, 0], X_train[:, 1], .8)plt.title('Negative log-likelihood predicted by a GMM')plt.axis('tight')plt.show() |
Total running time of the script: (0 minutes 0.219 seconds)
Download Python source code:
plot_gmm_pdf.py
Download IPython notebook:
plot_gmm_pdf.ipynb
Please login to continue.