An example to illustrate multi-output regression with decision tree.
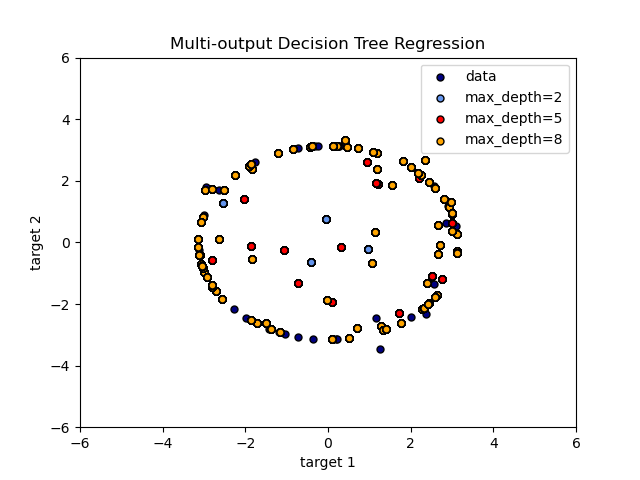
The decision trees is used to predict simultaneously the noisy x and y observations of a circle given a single underlying feature. As a result, it learns local linear regressions approximating the circle.
We can see that if the maximum depth of the tree (controlled by the max_depth parameter) is set too high, the decision trees learn too fine details of the training data and learn from the noise, i.e. they overfit.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | print(__doc__)import numpy as npimport matplotlib.pyplot as pltfrom sklearn.tree import DecisionTreeRegressor# Create a random datasetrng = np.random.RandomState(1)X = np.sort(200 * rng.rand(100, 1) - 100, axis=0)y = np.array([np.pi * np.sin(X).ravel(), np.pi * np.cos(X).ravel()]).Ty[::5, :] += (0.5 - rng.rand(20, 2))# Fit regression modelregr_1 = DecisionTreeRegressor(max_depth=2)regr_2 = DecisionTreeRegressor(max_depth=5)regr_3 = DecisionTreeRegressor(max_depth=8)regr_1.fit(X, y)regr_2.fit(X, y)regr_3.fit(X, y)# PredictX_test = np.arange(-100.0, 100.0, 0.01)[:, np.newaxis]y_1 = regr_1.predict(X_test)y_2 = regr_2.predict(X_test)y_3 = regr_3.predict(X_test)# Plot the resultsplt.figure()s = 50plt.scatter(y[:, 0], y[:, 1], c="navy", s=s, label="data")plt.scatter(y_1[:, 0], y_1[:, 1], c="cornflowerblue", s=s, label="max_depth=2")plt.scatter(y_2[:, 0], y_2[:, 1], c="c", s=s, label="max_depth=5")plt.scatter(y_3[:, 0], y_3[:, 1], c="orange", s=s, label="max_depth=8")plt.xlim([-6, 6])plt.ylim([-6, 6])plt.xlabel("target 1")plt.ylabel("target 2")plt.title("Multi-output Decision Tree Regression")plt.legend()plt.show() |
Total running time of the script: (0 minutes 0.221 seconds)
Download Python source code:
plot_tree_regression_multioutput.py
Download IPython notebook:
plot_tree_regression_multioutput.ipynb
Please login to continue.