discriminant_analysis.LinearDiscriminantAnalysis()

class sklearn.discriminant_analysis.LinearDiscriminantAnalysis(solver='svd', shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001) [source]

Linear Discriminant Analysis

A classifier with a linear decision boundary, generated by fitting class conditional densities to the data and using Bayes? rule.

The model fits a Gaussian density to each class, assuming that all classes share the same covariance matrix.

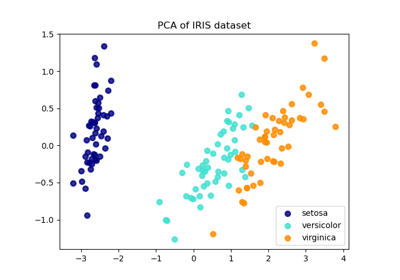
The fitted model can also be used to reduce the dimensionality of the input by projecting it to the most discriminative directions.

New in version 0.17: LinearDiscriminantAnalysis.

Read more in the User Guide.

Parameters:

solver : string, optional Solver to use, possible values: ?svd?: Singular value decomposition (default). Does not compute the covariance matrix, therefore this solver is recommended for data with a large number of features. ?lsqr?: Least squares solution, can be combined with shrinkage. ?eigen?: Eigenvalue decomposition, can be combined with shrinkage. shrinkage : string or float, optional Shrinkage parameter, possible values: None: no shrinkage (default). 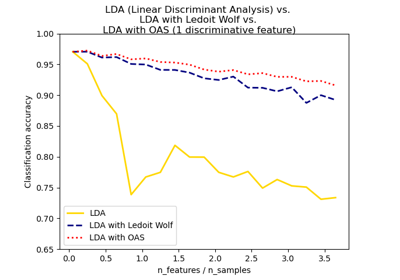?auto?: automatic shrinkage using the Ledoit-Wolf lemma. float between 0 and 1: fixed shrinkage parameter. Note that shrinkage works only with ?lsqr? and ?eigen? solvers. priors : array, optional, shape (n_classes,) Class priors. n_components : int, optional Number of components (< n_classes - 1) for dimensionality reduction. store_covariance : bool, optional Additionally compute class covariance matrix (default False). New in version 0.17. tol : float, optional Threshold used for rank estimation in SVD solver. New in version 0.17.

Attributes:

coef_ : array, shape (n_features,) or (n_classes, n_features) Weight vector(s). intercept_ : array, shape (n_features,) Intercept term. covariance_ : array-like, shape (n_features, n_features) Covariance matrix (shared by all classes). explained_variance_ratio_ : array, shape (n_components,) Percentage of variance explained by each of the selected components. If n_components is not set then all components are stored and the sum of explained variances is equal to 1.0. Only available when eigen or svd solver is used. means_ : array-like, shape (n_classes, n_features) Class means. priors_ : array-like, shape (n_classes,) Class priors (sum to 1). scalings_ : array-like, shape (rank, n_classes - 1) Scaling of the features in the space spanned by the class centroids. xbar_ : array-like, shape (n_features,) Overall mean. classes_ : array-like, shape (n_classes,) Unique class labels.

See also

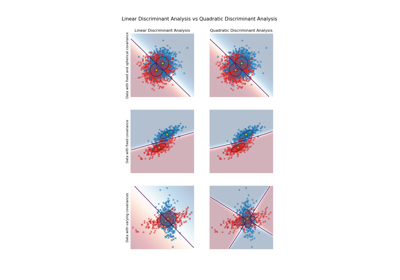
sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis

Quadratic Discriminant Analysis

Notes

The default solver is ?svd?. It can perform both classification and transform, and it does not rely on the calculation of the covariance matrix. This can be an advantage in situations where the number of features is large. However, the ?svd? solver cannot be used with shrinkage.

The ?lsqr? solver is an efficient algorithm that only works for classification. It supports shrinkage.

The ?eigen? solver is based on the optimization of the between class scatter to within class scatter ratio. It can be used for both classification and transform, and it supports shrinkage. However, the ?eigen? solver needs to compute the covariance matrix, so it might not be suitable for situations with a high number of features.

Examples

>>> import numpy as np
>>> from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = LinearDiscriminantAnalysis()
>>> clf.fit(X, y)
LinearDiscriminantAnalysis(n_components=None, priors=None, shrinkage=None,
              solver='svd', store_covariance=False, tol=0.0001)
>>> print(clf.predict([[-0.8, -1]]))
[1]

Methods

decision_function(X)	Predict confidence scores for samples.
fit(X, y[, store_covariance, tol])	Fit LinearDiscriminantAnalysis model according to the given training data and parameters.
fit_transform(X[, y])	Fit to data, then transform it.
get_params([deep])	Get parameters for this estimator.
predict(X)	Predict class labels for samples in X.
predict_log_proba(X)	Estimate log probability.
predict_proba(X)	Estimate probability.
score(X, y[, sample_weight])	Returns the mean accuracy on the given test data and labels.
set_params(\*\*params)	Set the parameters of this estimator.
transform(X)	Project data to maximize class separation.

__init__(solver='svd', shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001) [source]

decision_function(X) [source]

Predict confidence scores for samples.

The confidence score for a sample is the signed distance of that sample to the hyperplane.

Parameters:	X : {array-like, sparse matrix}, shape = (n_samples, n_features) Samples.
Returns:	array, shape=(n_samples,) if n_classes == 2 else (n_samples, n_classes) : Confidence scores per (sample, class) combination. In the binary case, confidence score for self.classes_[1] where >0 means this class would be predicted.

fit(X, y, store_covariance=None, tol=None) [source]

Fit LinearDiscriminantAnalysis model according to the given

training data and parameters.

Changed in version 0.17: Deprecated store_covariance have been moved to main constructor.

Changed in version 0.17: Deprecated tol have been moved to main constructor.

Parameters:	X : array-like, shape (n_samples, n_features) Training data. y : array, shape (n_samples,) Target values.

fit_transform(X, y=None, **fit_params) [source]

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters:	X : numpy array of shape [n_samples, n_features] Training set. y : numpy array of shape [n_samples] Target values.
Returns:	X_new : numpy array of shape [n_samples, n_features_new] Transformed array.

get_params(deep=True) [source]

Get parameters for this estimator.

Parameters:	deep : boolean, optional If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:	params : mapping of string to any Parameter names mapped to their values.

predict(X) [source]

Predict class labels for samples in X.

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	C : array, shape = [n_samples] Predicted class label per sample.

predict_log_proba(X) [source]

Estimate log probability.

Parameters:	X : array-like, shape (n_samples, n_features) Input data.
Returns:	C : array, shape (n_samples, n_classes) Estimated log probabilities.

predict_proba(X) [source]

Estimate probability.

Parameters:	X : array-like, shape (n_samples, n_features) Input data.
Returns:	C : array, shape (n_samples, n_classes) Estimated probabilities.

score(X, y, sample_weight=None) [source]

Returns the mean accuracy on the given test data and labels.

In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.

Parameters:	X : array-like, shape = (n_samples, n_features) Test samples. y : array-like, shape = (n_samples) or (n_samples, n_outputs) True labels for X. sample_weight : array-like, shape = [n_samples], optional Sample weights.
Returns:	score : float Mean accuracy of self.predict(X) wrt. y.

set_params(**params) [source]

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form <component>__<parameter> so that it?s possible to update each component of a nested object.

Returns:	self :

transform(X) [source]

Project data to maximize class separation.

Parameters:	X : array-like, shape (n_samples, n_features) Input data.
Returns:	X_new : array, shape (n_samples, n_components) Transformed data.

Examples using sklearn.discriminant_analysis.LinearDiscriminantAnalysis

Normal and Shrinkage Linear Discriminant Analysis for classification

Linear and Quadratic Discriminant Analysis with confidence ellipsoid

Comparison of LDA and PCA 2D projection of Iris dataset

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap...