linear_model.TheilSenRegressor()

class sklearn.linear_model.TheilSenRegressor(fit_intercept=True, copy_X=True, max_subpopulation=10000.0, n_subsamples=None, max_iter=300, tol=0.001, random_state=None, n_jobs=1, verbose=False) [source]

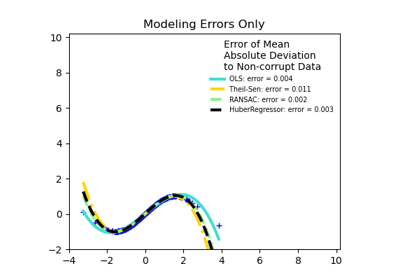
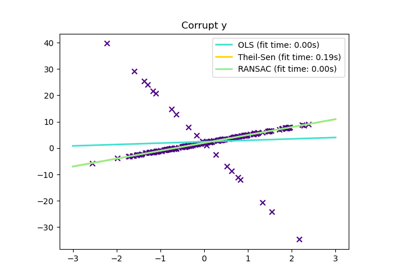
Theil-Sen Estimator: robust multivariate regression model.

The algorithm calculates least square solutions on subsets with size n_subsamples of the samples in X. Any value of n_subsamples between the number of features and samples leads to an estimator with a compromise between robustness and efficiency. Since the number of least square solutions is ?n_samples choose n_subsamples?, it can be extremely large and can therefore be limited with max_subpopulation. If this limit is reached, the subsets are chosen randomly. In a final step, the spatial median (or L1 median) is calculated of all least square solutions.

Read more in the User Guide.

Parameters:

fit_intercept : boolean, optional, default True Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations. copy_X : boolean, optional, default True If True, X will be copied; else, it may be overwritten. max_subpopulation : int, optional, default 1e4 Instead of computing with a set of cardinality ?n choose k?, where n is the number of samples and k is the number of subsamples (at least number of features), consider only a stochastic subpopulation of a given maximal size if ?n choose k? is larger than max_subpopulation. For other than small problem sizes this parameter will determine memory usage and runtime if n_subsamples is not changed. n_subsamples : int, optional, default None Number of samples to calculate the parameters. This is at least the number of features (plus 1 if fit_intercept=True) and the number of samples as a maximum. A lower number leads to a higher breakdown point and a low efficiency while a high number leads to a low breakdown point and a high efficiency. If None, take the minimum number of subsamples leading to maximal robustness. If n_subsamples is set to n_samples, Theil-Sen is identical to least squares. max_iter : int, optional, default 300 Maximum number of iterations for the calculation of spatial median. tol : float, optional, default 1.e-3 Tolerance when calculating spatial median. random_state : RandomState or an int seed, optional, default None A random number generator instance to define the state of the random permutations generator. n_jobs : integer, optional, default 1 Number of CPUs to use during the cross validation. If -1, use all the CPUs. verbose : boolean, optional, default False Verbose mode when fitting the model.

Attributes:

coef_ : array, shape = (n_features) Coefficients of the regression model (median of distribution). intercept_ : float Estimated intercept of regression model. breakdown_ : float Approximated breakdown point. n_iter_ : int Number of iterations needed for the spatial median. n_subpopulation_ : int Number of combinations taken into account from ?n choose k?, where n is the number of samples and k is the number of subsamples.

References

• Theil-Sen Estimators in a Multiple Linear Regression Model, 2009 Xin Dang, Hanxiang Peng, Xueqin Wang and Heping Zhang http://home.olemiss.edu/~xdang/papers/MTSE.pdf

Methods

decision_function(\*args, \*\*kwargs)	DEPRECATED: and will be removed in 0.19.
fit(X, y)	Fit linear model.
get_params([deep])	Get parameters for this estimator.
predict(X)	Predict using the linear model
score(X, y[, sample_weight])	Returns the coefficient of determination R^2 of the prediction.
set_params(\*\*params)	Set the parameters of this estimator.

__init__(fit_intercept=True, copy_X=True, max_subpopulation=10000.0, n_subsamples=None, max_iter=300, tol=0.001, random_state=None, n_jobs=1, verbose=False) [source]

decision_function(*args, **kwargs) [source]

DEPRECATED: and will be removed in 0.19.

Decision function of the linear model.

Parameters:	X : {array-like, sparse matrix}, shape = (n_samples, n_features) Samples.
Returns:	C : array, shape = (n_samples,) Returns predicted values.

fit(X, y) [source]

Fit linear model.

Parameters:	X : numpy array of shape [n_samples, n_features] Training data y : numpy array of shape [n_samples] Target values
Returns:	self : returns an instance of self.

get_params(deep=True) [source]

Get parameters for this estimator.

Parameters:	deep : boolean, optional If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:	params : mapping of string to any Parameter names mapped to their values.

predict(X) [source]

Predict using the linear model

Parameters:	X : {array-like, sparse matrix}, shape = (n_samples, n_features) Samples.
Returns:	C : array, shape = (n_samples,) Returns predicted values.

score(X, y, sample_weight=None) [source]

Returns the coefficient of determination R^2 of the prediction.

The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.

Parameters:	X : array-like, shape = (n_samples, n_features) Test samples. y : array-like, shape = (n_samples) or (n_samples, n_outputs) True values for X. sample_weight : array-like, shape = [n_samples], optional Sample weights.
Returns:	score : float R^2 of self.predict(X) wrt. y.

set_params(**params) [source]

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form <component>__<parameter> so that it?s possible to update each component of a nested object.

Returns:	self :

Examples using sklearn.linear_model.TheilSenRegressor

Robust linear estimator fitting

Theil-Sen Regression